Contenu
- Définition - Que signifie transformation de Fourier?
- Introduction à Microsoft Azure et au nuage Microsoft | Tout au long de ce guide, vous apprendrez ce qu'est le cloud computing et comment Microsoft Azure peut vous aider à migrer et à exploiter votre entreprise à partir du cloud.
- Techopedia explique la transformation de Fourier
Définition - Que signifie transformation de Fourier?
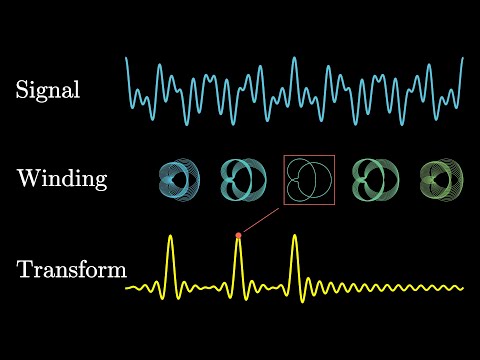
La transformée de Fourier est une fonction mathématique qui prend un modèle basé sur le temps en entrée et détermine le décalage de cycle global, la vitesse de rotation et la force pour chaque cycle possible dans le modèle donné. La transformation de Fourier est appliquée aux formes d'onde qui sont fondamentalement fonction du temps, de l'espace ou d'une autre variable. La transformée de Fourier décompose une forme d'onde en une sinusoïde et fournit ainsi un autre moyen de représenter une forme d'onde.
Introduction à Microsoft Azure et au nuage Microsoft | Tout au long de ce guide, vous apprendrez ce qu'est le cloud computing et comment Microsoft Azure peut vous aider à migrer et à exploiter votre entreprise à partir du cloud.
Techopedia explique la transformation de Fourier
La transformée de Fourier est une fonction mathématique qui décompose une forme d'onde, fonction du temps, en fréquences qui la composent. Le résultat produit par la transformée de Fourier est une fonction complexe de la fréquence. La valeur absolue de la transformée de Fourier représente la valeur de fréquence présente dans la fonction d'origine et son argument complexe représente le déphasage du sinusoïdal de base dans cette fréquence.
La transformée de Fourier est également appelée une généralisation de la série de Fourier. Ce terme peut également être appliqué à la fois à la représentation du domaine fréquentiel et à la fonction mathématique utilisée. La transformée de Fourier aide à étendre la série de Fourier aux fonctions non périodiques, ce qui permet de visualiser n'importe quelle fonction comme une somme de simples sinusoïdes.
La transformée de Fourier d'une fonction f (x) est donnée par:

Où F (k) peut être obtenu en utilisant la transformée de Fourier inverse.
Certaines des propriétés de la transformation de Fourier incluent:
- C'est une transformée linéaire - Si g (t) et h (t) sont deux transformées de Fourier données respectivement par G (f) et H (f), alors la transformée de Fourier de la combinaison linéaire de g et t peut être facilement calculée.
- Propriété de décalage temporel - La transformée de Fourier de g (t – a) où a est un nombre réel qui décale la fonction initiale a la même quantité de décalage dans l'amplitude du spectre.
- Propriété de modulation - Une fonction est modulée par une autre fonction lorsqu'elle est multipliée dans le temps.
- Théorème de Parseval - La transformée de Fourier est unitaire, c’est-à-dire que la somme du carré d’une fonction g (t) est égale à la somme du carré de sa transformée de Fourier, G (f).
- Dualité - Si g (t) a la transformée de Fourier G (f), alors la transformée de Fourier de G (t) est g (-f).